The Dynamics of Insight

Imagine a billiard ball bouncing around a multi-sided table. Not a familiar rectangle with felt and pockets, but a frictionless polygon where the ball, unimpeded by mass or spin, travels forever, bouncing off the edges at perfect angles. That simple image captivated William Veech, a mathematician who spent his life transforming such deceptively basic questions into rich mathematical insight.

Veech, who held Rice’s Edgar Odell Lovett Chair in Mathematics until his death in 2016, approached research with unusual independence. He never co-authored a paper, believing that every person should develop a unique perspective. Yet far from being isolated, Veech was deeply connected — mathematically, intellectually and personally.

“He was historically known for being the solo-author person,” said former student Jonathan Fickenscher ’11. “But he was still very engaged and active in the math community, just in a different way.” Despite working alone, Veech’s ideas forged powerful connections between fields and continue to shape a field that barely existed before him.

At the heart of Veech’s work was the study of dynamical systems, which describe how mathematical structures evolve over time. He was interested in patterns that might emerge when you take a simple system and ask what happens in the long run. Frictionless billiards provided one such system.

What made these billiards more than a curiosity was the complexity of the ball’s path. Depending on the table’s shape and the ball’s starting angle, the ball might bounce off the walls several times and return to its starting point, tracing the same periodic path over and over again. Or it might cover the entire table, spending equal time in every region of the table. Or it might do something in between — visiting some parts more than others, never repeating and never distributing evenly.

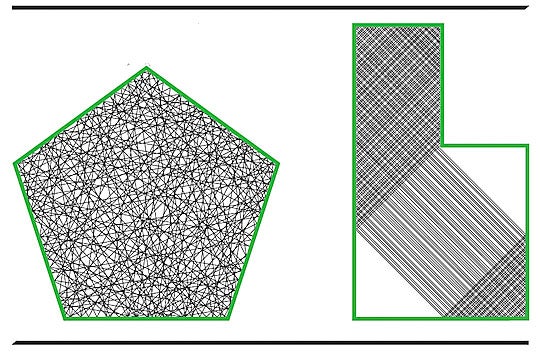
On familiar rectangular tables, only the two simplest behaviors occur: every trajectory either loops or spreads out evenly. But what might happen on a table shaped like a regular pentagon? Or a right triangle?

Veech found a way to understand these systems by translating the problem into a new kind of geometry. His breakthrough came with what are now called Veech surfaces: flat geometric surfaces where the trajectories of these billiard paths can be studied with precision. Idealized billiard trajectories on these surfaces obey familiar reflection rules. But the table can be any polygon with angles that are rational multiples of pi, and the ball never slows or stops.

Veech discovered that for some of these shapes — the regular n-gons, a shape with n sides where all sides are the same length and all angles are the same — every single trajectory on the surface must be either periodic or uniformly distributed. There were no intermediate behaviors. This clean division became known as the Veech dichotomy. “Every trajectory is either closed or uniformly distributed,” said Jonathan Chaika ’10, who joins the Rice faculty as a professor of mathematics this year. “It’s a simple, beautiful rule.”

Understanding why this happens required thinking beyond billiard tables. The key was to look not at the table itself, but at how its symmetries translated into the geometry of an associated surface. If a table could be unfolded into a surface where straight-line motion corresponded to the billiard ball’s path, you could analyze the motion as a kind of flow across the surface. These special surfaces turned out to have remarkable regularities and symmetries, governed by what is now called the Veech group.

Veech surfaces provide a way to visualize these trajectories, but they began with a seemingly unrelated, abstract idea called interval exchange transformations — a simple model that is good for understanding basic dynamical phenomena. Here, you start with a line divided into a handful of smaller segments, which can be rearranged by cutting the line into pieces and reassembling those pieces in a new order. This is like cutting up a paper strip, rearranging the pieces, and taping them back together — a process you repeat over and over to observe how the pattern evolves. While this sounds simple, the patterns that emerge when you repeat the transformation many times can become complex and rich, allowing mathematicians to model systems that evolve over time by slicing them into simpler parts.

To visualize and analyze these interval exchanges better, Veech developed a method to represent them geometrically as flat, two-dimensional surfaces. By “suspending” a surface over these intervals, mathematicians could study trajectories as straight-line flows on these surfaces rather than abstract interval rearrangements.

This geometric perspective allowed deeper insights and linked interval exchanges to other mathematical fields. “He developed a series of connections from these interval exchange transformations to billiards,” said David Fisher, Rice’s Milton B. Porter Professor of Mathematics. “He started from a simple model that you can prove things about and then walked through a door into this giant world that he just built up.”

Over time, Veech’s groundbreaking ideas laid the foundation for a broader field called Teichmüller dynamics. This area looks at how surfaces change and evolve when subjected to transformations like stretching and rotating. Instead of studying just one surface, mathematicians explore an entire space made up of all possible versions of a surface with the same basic shape. Just as we can visualize one-dimensional trajectories sitting in two-dimensional polygons, we can imagine those surfaces themselves existing inside an even higher-dimensional space. Teichmüller dynamics helps us understand how flows — like the path of a billiard ball — behave as you move through this space. Veech, along with mathematician Howard Masur, helped build the foundations of this field.

“You have these individual dynamical systems that are balls bouncing in these little tables,” Fisher said. “And suddenly, almost of their own volition, all of these possible billiard tables become embedded in a gigantic, bigger dynamical system that’s called Teichmüller dynamics. Veech saw a connection between that and what he was thinking about with billiards, but he really saw how this connected to other problems in dynamical systems.”

This framework paved the way for later breakthroughs. One of the most famous is the “magic wand theorem” proved by Alex Eskin and Maryam Mirzakhani. It imagines a perfectly mirrored room — like a polygonal billiard table — and asks whether light from a single source will eventually illuminate the whole room. The theorem showed that for rational-angled rooms, the light eventually illuminates every point in the room except for finitely many blind spots.

“Maryam won the Fields Medal in part for this theorem, and Eskin won the Breakthrough Prize for this theorem,” Fisher said. “It’s a gigantic result, and I don’t think people would’ve been looking for it without Veech. He laid the foundations on which all this other stuff could be discovered.”

Veech’s mentoring style matched his mathematics: open, exploratory and patient. He didn’t assign problems. He offered possibilities. “His style was not to tell you what to do,” said Fickenscher, who is now a senior lecturer of mathematics at Princeton University. “He’d always give me different papers to look at, and when I wasn’t sure what was going on with something, he’d come back with a whole new library of choices. He just said this was part of the process. By the time I got to the thing I was working on, I was really involved. That would not have been the same if it was something handed to me.”

Chaika had a similar experience. “I would come in with some problem I’d been thinking about for a long time. He would always have time for me. I’d blather at him for 20 minutes or an hour, and then he would pause for a moment and say ‘Have you thought about this thing?’ And it would be something I had never thought about before and would seem to me like it had nothing to do with it,” he said. “Then sometime about a month later, my brain would finally catch up to it and be like, ‘Oh, that’s deep.’”

Veech’s generosity extended beyond math. He cultivated a sense of calm and care that made students feel safe enough to think freely. Fickenscher remembered one quiet lunch in Veech’s office on a visit after he graduated, when wires got crossed and no lunch plans were on his schedule. “He always had this fruit bowl on his desk. So that lunch was me sitting with my advisor just peeling oranges and chatting about things since my departure,” he said. “I try very hard with the students I advise at Princeton to give them the ability to believe that it’s okay to take a breath and take some time.”

He may never have co-authored a paper, but Veech was part of an ongoing mathematical dialogue with colleagues. “He believed that people should have their own unique perspective towards mathematics,” Chaika said. “I think that shows in his own work, but he was definitely influenced by other people.” Veech was motivated by his Rice colleagues, like the late mathematics professor Michael Boshernitzan, writing “companion papers” on related topics and sharing ideas freely without coauthoring.

The work Veech began is taking new root at Rice. After a lull in activity in the subject, the department is reinvesting in dynamics. Fisher joined the faculty in 2022, and with the recent addition of Chaika and Francisco Arana-Herrera — both of whom work on problems closely connected to the legacies of Veech and Boshernitzan, including billiards — Rice again has a thriving group in the field Veech helped shape.

“We weren’t trying to replace Veech and Boshernitzan as a pair. But we have. For many of us, there’s a certain poetry in that,” Fisher said. “The intellectual history of this subject was built at Rice. It’s a thriving and important area of mathematics that we can keep alive at Rice.”

Just as a single trajectory on a Veech surface can fill the table or return to its start, Veech’s own path continues outward, radiating through the mathematics he pioneered, the students he inspired and the questions he left behind.

“He saw beauty in mathematics in a really wonderful way, and especially in the interactions between multiple types of mathematics — geometry, complex analysis, dynamics — all coming together,” said Chaika. “And he had the taste and courage to pursue what he saw as beautiful.”